基于生成对抗网络的高光谱图像分类半监督学习
原文:《Generative Adversarial Networks-Based Semi-Supervised Learning for Hyperspectral Image Classification》
核心思想
- 采用三维双边滤波器(3DBF),通过将HSI自然处理为体积数据集来提取光谱空间特征。通过3DBF将空间信息集成到提取的特征中,这有利于后续的分类步骤
- 在半监督学习的频谱空间特征上训练GAN。GAN包含两个相互对立训练的神经网络(即生成器和鉴别器)
主要问题
- 许多无监督方法,如模糊聚类、模糊C-均值方法、人工免疫算法、基于图的方法,如果先验知识太少,就无法确保集群和类之间的关系。
- 典型的监督分类器包括支持向量机(SVM)、人工神经网络(ANN)和基于稀疏表示的分类(SRC)等,它们的性能在很大程度上取决于标记样本的数量。与标记样本的迫切需求相反,他们忽略了大量未标记样本以帮助分类。
半监督方法四种类型
- 生成模型,其估计条件密度以获得未标记样本的标签。
- 低密度分离,其目的是在存在少量样本(标记或未标记)的区域设置边界。最先进的算法之一是转导支持向量机(TSVM)。
- 基于图的方法,该方法利用标记和未标记的样本来构建图并最小化能量函数,从而将标签分配给未标记的样品。
- 基于包装器的方法,迭代地应用监督学习方法,并且在每次迭代中标记一定数量的未标记样本。自训练和联合训练算法是常用的基于包装器的方法。
本文方法
- 通过3DBF提取光谱空间特征。与基于向量/矩阵的方法相比,3DBF提取的结构特征可以通过自然遵循HSI的3D形式并将3D立方体视为一个整体来有效地保存光谱空间信息。
- 由GAN以半监督的方式对HSI进行分类。与监督方法相比,GAN可以利用有限的训练样本和大量的未标记样本。与非对抗性网络相比,GAN利用区分模型来训练基于博弈论的生成网络。
整体框架
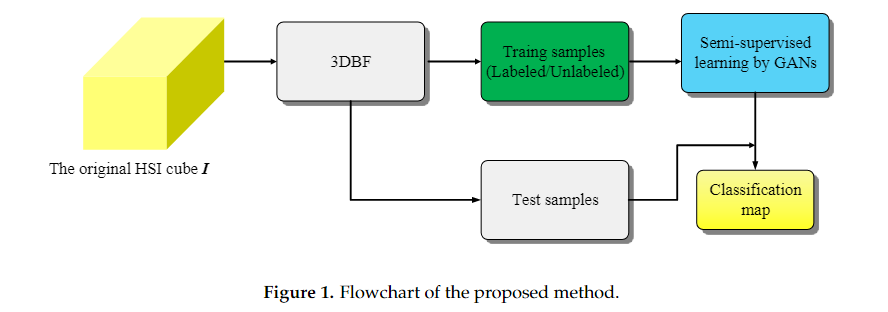
该方法的概念框架如图1所示,由两部分组成:(1)特征提取;(2)半监督学习。原始HSI立方体I的光谱空间特征可以通过3DBF提取,3DBF是一个3D滤波器,可以遵循HSI的3D特性,同时提取光谱空间特征。随后,通过充分利用有限的标记样本和足够的未标记样本,在特征空间中使用GAN进行半监督分类。分类图可以通过可视化不同样本的分类结果来实现。将空间信息纳入高光谱分类有助于提高分类器的性能,基于3D/张量的方法比基于向量/矩阵的方法更有效地提取联合频谱空间结构信息。
三维双向滤波器提取光谱空间特征
在本文中,将双边滤波器扩展到3DBF,用于HSI体积数据的光谱空间特征提取。
 假设原始立方体为
假设原始立方体为
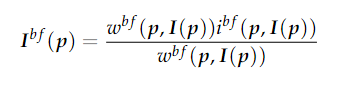 其中函数
其中函数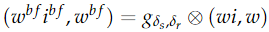 在高光谱图像中,3D图像域(即空光域
在高光谱图像中,3D图像域(即空光域
- 在
上,用定义的高斯函数卷积 和 ,在这步中, 和 分别模糊为 和 ; - 将
除以 得到 ; - 在
上计算 的值得到滤波结果
3DBF还可以通过上采样下采样来加速,示意图如下: 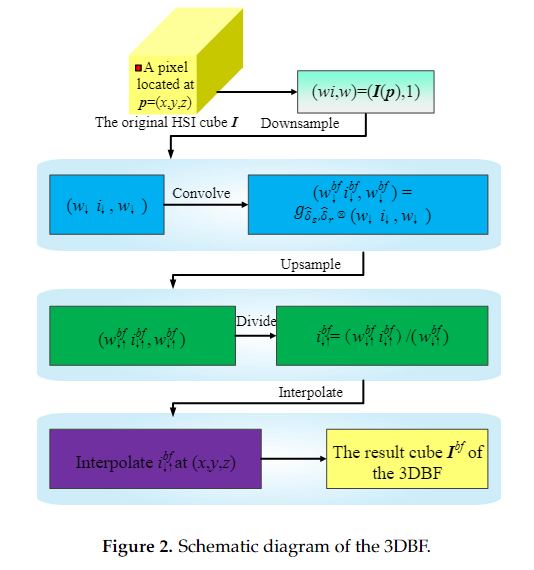
基于生成对抗网络的HSI半监督分类
GAN简介
GAN是新提出的基于对抗性网络的深度架构,以对抗性方式训练模型以生成模拟特定分布的数据。与其他深度学习方法不同,GAN是一个围绕两个功能的架构(见图3),即生成器G,它可以将样本从随机均匀分布映射到数据分布,以及鉴别器D,它被训练来区分样本是否属于真实数据分布。在GAN中,生成器和鉴别器是基于博弈论共同学习的。生成器G和鉴别器D可以以交替的方式训练。在每个步骤中,G从可能欺骗D的随机噪声z中产生一个样本,然后向D呈现真实数据样本以及G生成的样本,以将样本分类为“真”或“伪”。随后,G因生产出能够“欺骗”D和D以进行正确分类的样本而获得奖励,两个函数都被更新,直到达到纳什均衡,迭代停止。
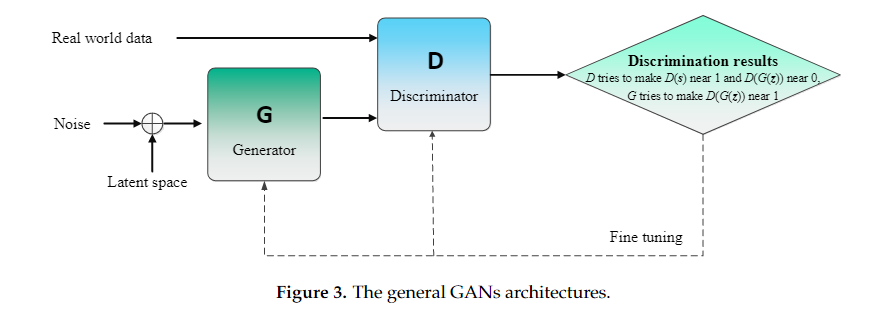
用于分类的生成对抗网络
为了建立基于GAN的新的半监督高光谱分类框架,我们将生成的样本添加到HSI数据集,并将其表示为第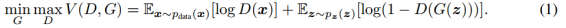 未标记的训练样本属于前
未标记的训练样本属于前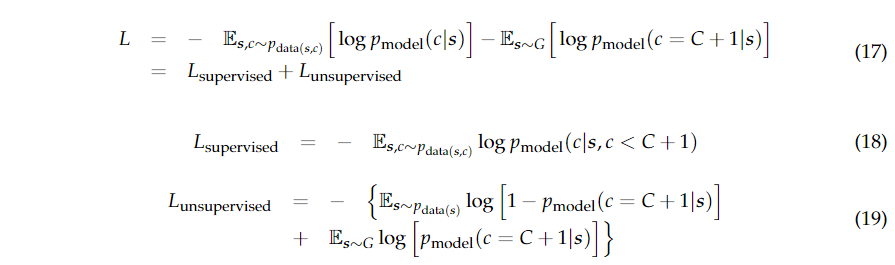 其中,
其中,