基于半监督广义学习系统的高光谱图像分类
原文:《Hyperspectral Imagery Classification Based on Semi-Supervised Broad Learning System》
主要思路
深度学习
- 方法需要复杂的结构调整和大量的网络训练计算。
- 存在标记样本数量有限的问题。
针对这些问题,Chen和Liu[20]提出了一种新的广义学习系统(BLS),提供一种可选的学习方法。该方法基于随机向量函数链接神经网络(RVFLNN)。首先,将原始数据通过随机权重映射为映射特征(MF),并存储在特征节点中。接下来,同样通过随机权重映射MF,得到增强节点(EN)进行广泛展开。最后,用岭回归逼近法求解
基于图的SSL方法
- 算法性能受所构造图的影响较大。
- 相邻参数具有较高的灵敏度。
考虑数据类结构,Shao, et al.[28]提出了一个类概率(CP)结构,它可以通过类概率矩阵来表示每个样本与每个类之间的关系。本文采用此方法。
本文方法
提出了一种基于半监督BLS(半监督BLS)的HSI分类方法。
- 这是第一次尝试将BLS应用于HSI分类任务。所提出的SBLS可以获得更高的HSI分类精度和更快的训练速度。
- 在扩展半监督BLS中引入类概率结构,既能利用有限数量的标记样本,又能利用大量的未标记样本。
基于SBLS的HSI分类
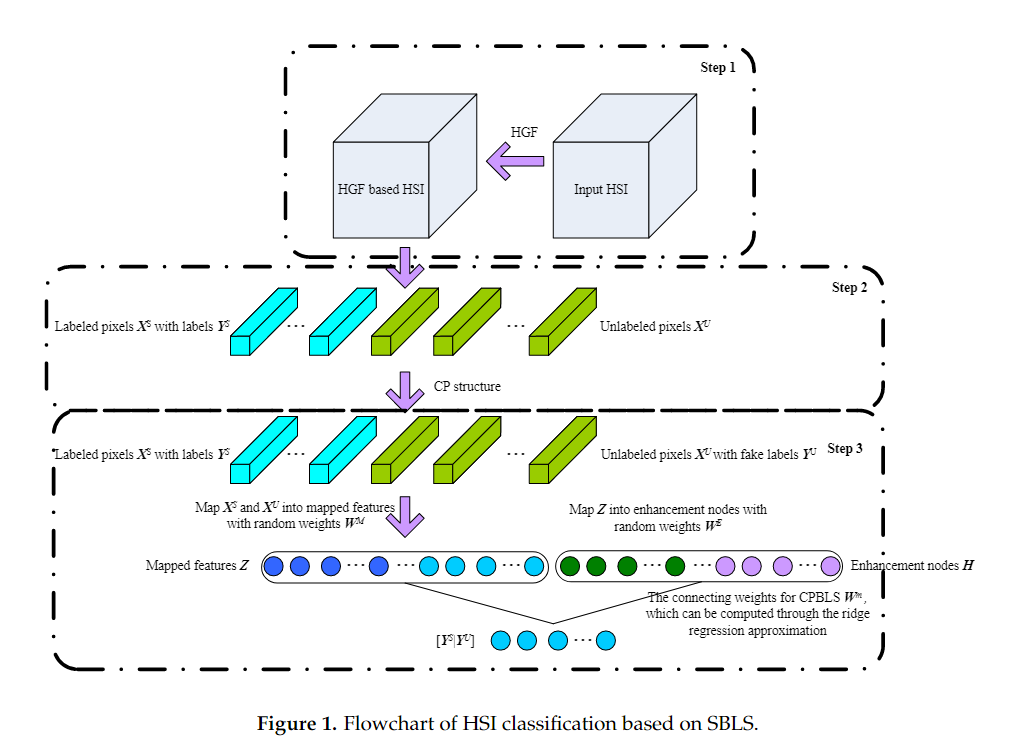
基于SBLS的HSI分类流程图如图1所示,包括三个步骤:(1)对原始HSI数据进行分层制导滤波(HGF)处理,得到HSI的光谱-空间表示;(2)通过CP结构得到未标记样本的伪标签;(3)通过标记样本和相应的标签,以及未标记样本和相应的伪标签来训练SBLS。
分层制导滤波
SBLS的第一步是得到HSI的HGF表示,如图1中的步骤1所示。原始高光谱图像以3D张量的形式表示。如果用张量来表示向量化,不仅数据维度大大增加,而且固有的数据结构也会被破坏。潘等人[29]提出了一种基于HGF的HSI数据的光谱空间表达方法。作为一种边缘保持滤波方法,HGF能够在保持图像整体结构的同时去除噪声和小细节,从而将原始HSI数据映射到具有更丰富特征表达的特征子空间。利用HGF的优越性,对原始HSI进行处理,得到HSI的光谱-空间表达。
作为制导滤波和滚动制导滤波的扩展,HGF可以生成一系列的联合光谱-空间特征。HGF最小化以下能量函数:
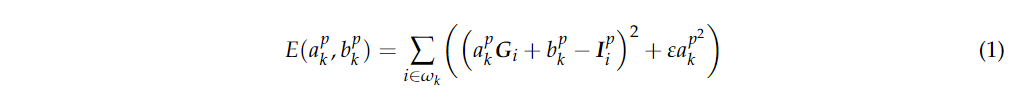 其中,
其中,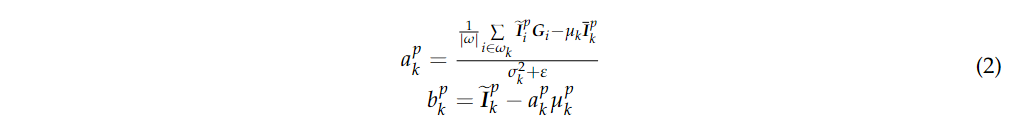 其中
其中
类别概率结构
SBLS的第二步是通过CP结构得到未标记样本的伪标签,如图1中的步骤2所示。通过HGF表达式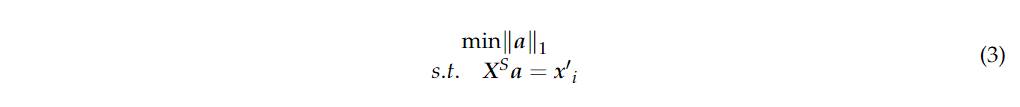 其中
其中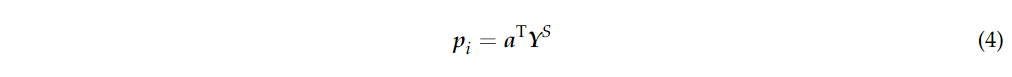 其中,
其中,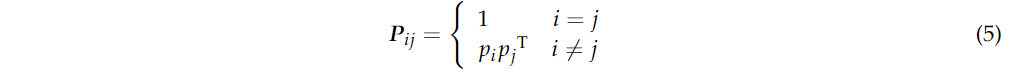 进一步,
进一步,
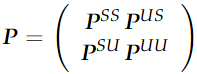
其中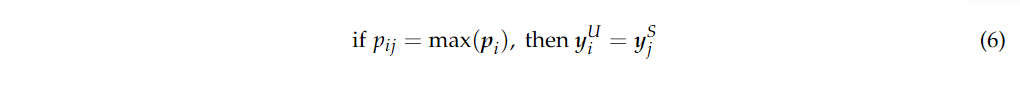
SBLS
SBLS的第三步是训练SBLS模型,得到未标记样本的预测标签,如图1中的步骤3所示。基于RVFLNN提出的BLS包括三个部分:映射特征(由输入映射而来)、增强节点(由映射特征映射而来)和输出标签(由映射特征与增强节点联合映射而成)。学习参数为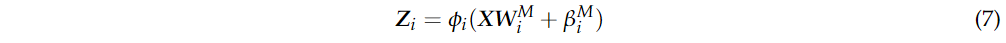 其中
其中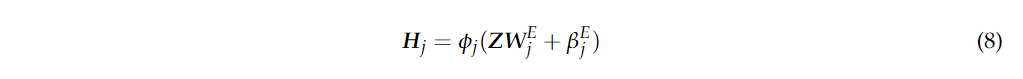 其中
其中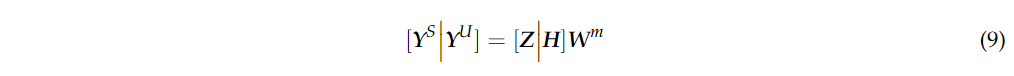 其中
其中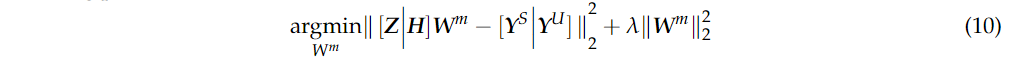
其中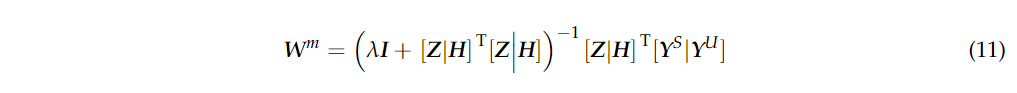 当
当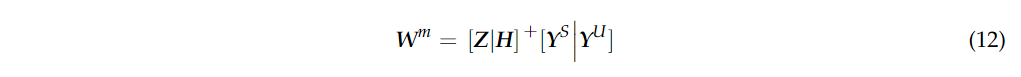 具体来说,我们有:
具体来说,我们有: 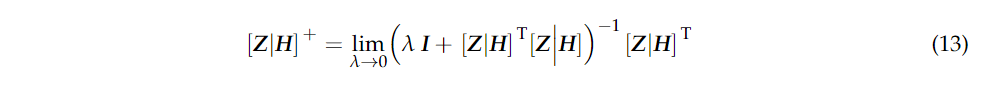 最后,预测标签可以通过以下方法获得:
最后,预测标签可以通过以下方法获得: 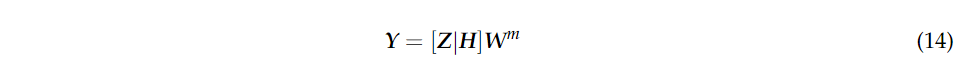 综上所述,基于SBLS的HSI分类算法步骤如表1所示。
综上所述,基于SBLS的HSI分类算法步骤如表1所示。  输入:基于HGF的HSI光谱-空间表示。
1.根据公式(5)计算类别概率矩阵
输入:基于HGF的HSI光谱-空间表示。
1.根据公式(5)计算类别概率矩阵