SoftMatch:解决半监督学习中的数量-质量权衡问题
原文:《SoftMatch: Addressing the Quantity-Quality Tradeoff in Semi-supervised Learning》
主要问题
- SSL的主要挑战在于如何有效地利用未标记数据的信息来提高模型的泛化性能。
- 具有置信度阈值的伪标记非常成功并被广泛采用,基于阈值的伪标签的核心思想是用预测置信度高于硬阈值的伪标签来训练模型,而其他的则被简单地忽略。然而,这种机制固有地表现出数量与质量的权衡,这破坏了学习过程。例如,FixMatch 中利用的高置信度阈值确保了伪标签的质量。然而,它丢弃了大量不自信但正确的伪标签。
- 动态增长的阈值或类阈值鼓励使用更多的伪标签,但不可避免地会完全使用可能误导训练的错误伪标签。例如,FlexMatch。
综上所述,具有置信度阈值的数量-质量权衡限制了未标记数据的利用率,这可能会阻碍模型的泛化性能。
解决方法:
- 所以作者提出softmatch的方法,采用截断高斯函数。根据我们对边缘分布的假设,采用一个截断的高斯函数来拟合置信度分布,该置信度分布根据伪标签的置信度与高斯均值的偏差,为可能正确的伪标签分配较低的权重。
- 通过统一对齐的方法来解决伪标签类不平衡的问题。
主要方法
我们正式定义了 SSL
中伪标签的数量和质量,并从统一样本权重公式的角度总结了先前方法中存在的固有权衡。我们首先确定数量-质量权衡背后的根本原因是缺乏加权函数对伪标签分布施加的复杂假设。其中,置信度阈值可以看作是根据样本的置信度分配二元权重的阶梯函数,它假设置信度高于阈值的伪标签是正确的,而其他伪标签是错误的。在分析的基础上,我们提出了SoftMatch来克服这种权衡,在训练过程中保持高数量和高质量的伪标签。根据我们对边缘分布的假设,采用一个截断的高斯函数来拟合置信度分布,该置信度分布根据伪标签的置信度与高斯均值的偏差,为可能正确的伪标签分配较低的权重。高斯函数的参数是在训练期间使用模型的历史预测来估计的。此外,我们提出了统一对齐的方法来解决伪标签中由于不同类别的学习困难而导致的不平衡问题。它进一步巩固了伪标签的数量,同时保持了伪标签的质量。在图1(c)和图1(b)所示的Two-Moon数据集中,SoftMatch获得了明显更好的伪标签精度,同时在训练过程中保持了始终较高的伪标签利用率,因此,可以获得如图1(d)所示的更好的学习决策边界。
 贡献可以概括为:
贡献可以概括为:
- 我们通过正式定义伪标签的数量和质量,以及它们之间的权衡,证明了统一加权函数的重要性。我们发现,以前的方法中固有的权衡主要源于对伪标签分布缺乏仔细的设计,这是由加权函数直接施加的。
- 我们提出了SoftMatch,以有效地利用低置信度但正确的伪标签,将截断的高斯函数拟合为置信度分布,从而克服了权衡。我们进一步提出统一对齐来解决假标签的不平衡问题,同时保持其高数量和高质量。
- 我们证明了SoftMatch在各种图像和文本评估设置上优于以前的方法。我们还通过经验验证了在SSL中追求更好的无标签数据利用率的同时保持伪标签的高精度的重要性。
重温 SSL 的数量-质量权衡
问题陈述
我们首先在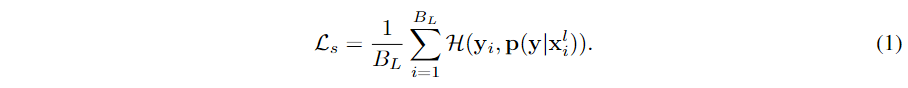 对于无监督损失,大多数现有的伪标签方法都利用置信度阈值机制来掩盖训练中不自信和可能不正确的伪标签。在本文中,我们更进一步,从样本加权的角度提出了一个统一的置信度阈值方案(以及其他方案)。具体来说,我们将无监督损失
对于无监督损失,大多数现有的伪标签方法都利用置信度阈值机制来掩盖训练中不自信和可能不正确的伪标签。在本文中,我们更进一步,从样本加权的角度提出了一个统一的置信度阈值方案(以及其他方案)。具体来说,我们将无监督损失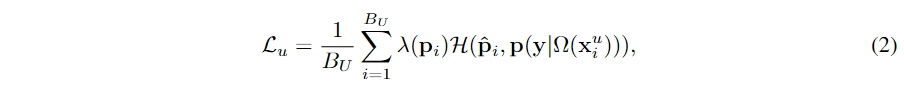 其中
其中
从样本加权的角度进行数量-质量权衡
定义 2.1(伪标签的数量):参加训练的伪标签的数量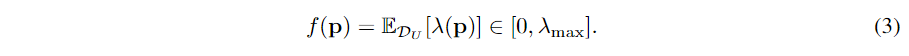 定义 2.2(伪标签的质量):质量
定义 2.2(伪标签的质量):质量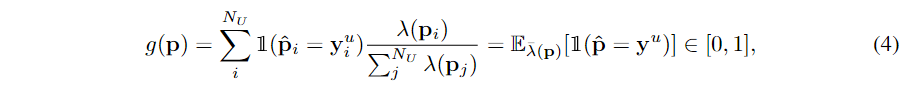 其中
其中
Softmatch
样本加权的高斯函数
与以前的方法本质上不同,我们通常假设边缘分布的基础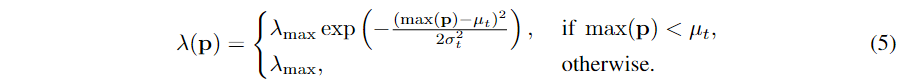 这也是一个在
这也是一个在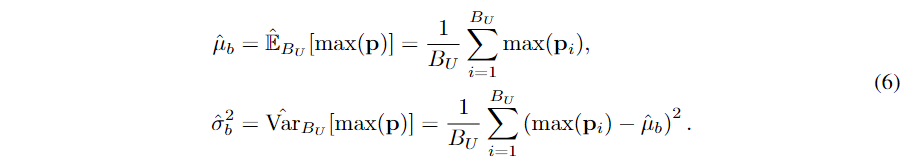 然后,我们使用动量为
然后,我们使用动量为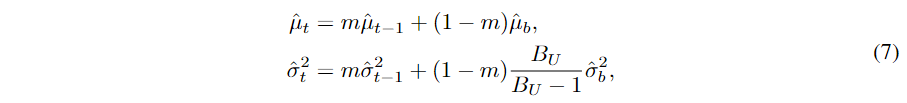 其中,我们对 EMA 使用无偏方差,并将
其中,我们对 EMA 使用无偏方差,并将
公平数量的统一对齐
由于不同的类别表现出不同的学习难度,生成的伪标签可能具有潜在的不平衡分布,这可能会限制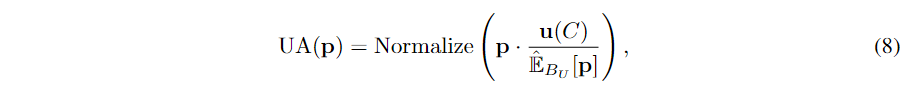 其中
其中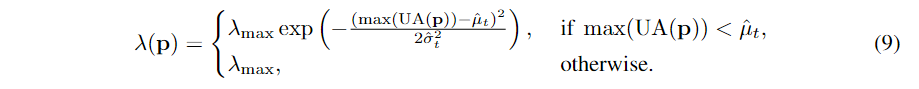 在计算样本权重时,UA
鼓励将较大的权重分配给预测较少的伪标签,将较小的权重分配给预测较多的伪标签,从而缓解不平衡问题。
UA与之前提出的分布对齐(DA)(Berthelot et al.,
2019a)之间的本质区别在于无监督损失的计算。归一化操作使预测概率偏向于预测较少的类。在
DA 中,这可能不是问题,因为归一化预测在交叉熵损失中用soft target。
然而,使用伪标签,标准化后可能会创建更多错误的伪标签,这会损害质量。UA
通过利用原始预测来计算伪标签和标准化预测来计算样本权重来避免这个问题,从而在
SoftMatch 中保持伪标签的数量和质量。 完整的训练算法如附录 A.2 所示。
补充:在训练过程中,我们首先计算未标记的数据在过去所有次预测中的平均值,我们称之为
在计算样本权重时,UA
鼓励将较大的权重分配给预测较少的伪标签,将较小的权重分配给预测较多的伪标签,从而缓解不平衡问题。
UA与之前提出的分布对齐(DA)(Berthelot et al.,
2019a)之间的本质区别在于无监督损失的计算。归一化操作使预测概率偏向于预测较少的类。在
DA 中,这可能不是问题,因为归一化预测在交叉熵损失中用soft target。
然而,使用伪标签,标准化后可能会创建更多错误的伪标签,这会损害质量。UA
通过利用原始预测来计算伪标签和标准化预测来计算样本权重来避免这个问题,从而在
SoftMatch 中保持伪标签的数量和质量。 完整的训练算法如附录 A.2 所示。
补充:在训练过程中,我们首先计算未标记的数据在过去所有次预测中的平均值,我们称之为
算法过程
我们在本节中介绍了 SoftMatch 的伪算法。 SoftMatch
采用截断高斯函数,在每个训练步骤从置信度分布的 EMA
估计参数,这引入了简单的计算。 